频谱分析仪应用解惑之带宽
发布时间：
2019-12-17 
浏览次数：
9097
次 
带宽是频域分析中的常见指标，频谱分析仪中常见的带宽有分辨率带宽和视频带宽，本文将全面讲解这些概念，以及之间的联系和区别。 
带宽是频域分析中的常见指标，频谱分析仪中常见的带宽有分辨率带宽和视频带宽，本文将全面讲解这些概念，以及之间的联系和区别。
分辨率带宽RBW(Resolution Bandwidth)，代表频谱分析仪将两个不同频率的信号清晰分辨出来的能力。两个不同频率的信号的距离如低于频谱分析仪的RBW，此时该两信号将部分重叠难以分辨。就像一幅图画在电脑上使用不同的分辨率去观察，清晰度是完全不同的。这里的“清晰”只是主观感受，普遍量化的标准是分辨率带宽定义在距离载波峰值衰减3dB的地方。在电磁干扰（EMI）测试标准中，分辨率带宽的标准为6dB。可以说6dB的选择性比3dB要强。
如图1所示是基于鼎阳科技SSA3032X频谱仪测量两个距离约20 kHz的单音信号，在使用带宽为30kHz，10kHz，3kHz的RBW观察时，这两个频率相近的信号测量的功率完全不变，信号被清晰分辨出来的程度是完全不同的。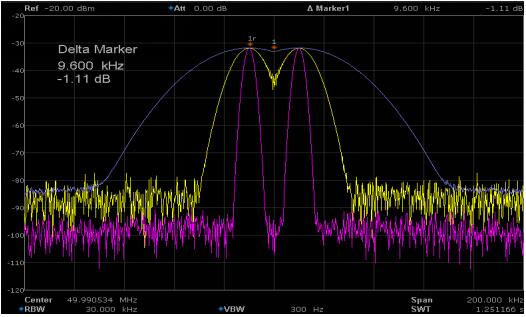
但是3dB带宽这个量化标准仍然是不够严谨，因为它只约束了3dB这一个点的位置。在相同的RBW下，还需要“矩形系数”这个参数，如图2所示。有的地方称为形状因子，就是衰减60dB时的带宽和衰减3dB时的带宽的比值。这个值越小越好，表明这个选择形状细长，能够将频率临近的信号完整地分离出来。一般来说，常见的数字频谱分析仪的矩形系数普遍为5：1左右。一个极端情况，如果3dB带宽和60dB带宽相同，那么矩形系数为1，这就是一个长方形了！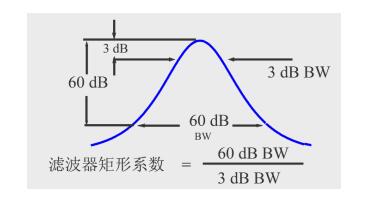
RBW的带宽和矩形系数，基本上决定了一个频谱分析仪的频率分辨能力，也就是将不等幅信号分辨出来的能力；反过来看，一旦RBW确定，那么是不能够观察到窄于RBW的频率谱线的。如图3所示，随着频率分辨能力的变化，两个临近的不等幅信号的分辨程度是不同的。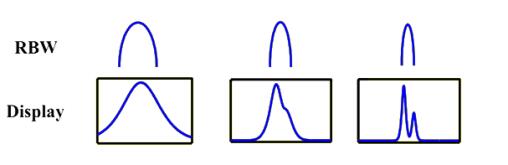
图3 RBW分辨不等幅信号的能力
当然，影响频谱分析仪频率分辨能力的因素不止这两个，在测量距离一个载波信号非常近的小信号时，即使RBW设置的相当小，也有可能分辨不出来。这是因为频率分辨能力还受到近端的相位噪声和本振的剩余调制的限制，这两点将在后续文章中阐述。
那么问题来了，为什么频谱分析仪的分辨率带宽的形状是一个脉冲的形状，而不能将理论上一个本来就很干净的正弦波检测为一根同样干净的细细的谱线？另一个相似的问题是，既然分辨率越清晰越好，为什么不直接使用最精细的分辨率带宽去检测信号？
面对这样的情况，一个训练有素的工程师对于很多理想化的测量场景，一定会给出的回答是：工程折中的实现。想以合适的代价得到测量结果，就不可避免丧失精度；反过来，想测得无比精确，结果就要付出很大成本才能得到。套用这个思路，我们给出一个官僚的解释：成本。
先回答第一个形状问题。这首先涉及到频谱分析仪的频率检测原理。从基础的角度考虑，我们可以把频谱分析仪理解为一种频率选择、峰值检测的电压表。“峰值检测”的表述，说明频谱分析仪的测量结果将是稳定的峰值，而不是变化的波形；“频率选择性”的表述，则说明频谱分析仪的对正弦波的频率是选择出来的，那么选择的方法其实就决定了频率分辨能力的大小。对于一些以FFT分析步进实现的频谱分析仪，只是每次选择的范围变大了一些，但是基本过程是没有根本变化的。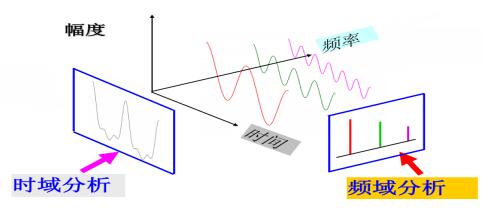
图 4 频域和时域的关系
在某个特定测量频率上看，我们对于频率的测量，就是用一个特定形状的滤波器去选频，一个细细的干净的正弦波经过选择滤波器，从而得到这个频率点的响应幅度，那么这个选择成型滤波器的选择能力就基本代表了频谱分析仪的频率选择能力。在整个频带测量过程上看，频谱分析仪的测量过程其实是使用穷举法，一个频点接一个频点地通过选择成型滤波器并测量峰值，然后遍历所有频点，拼凑出整个频率范围的能量分布。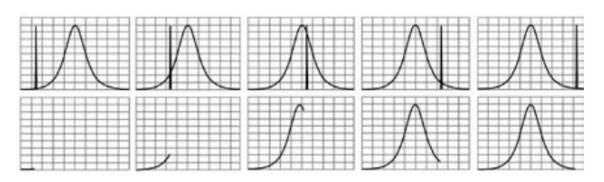
图 5成型滤波器移动选择频率
如此来说，极端细致分辨能力的滤波器，相当于使用一个冲击函数去选择出需要的频率。如何构造一个冲击函数形状的滤波器呢，它在时域上是时间无穷幅度不变的，也就是不可能构造出来。退一步讲，使用一个矩形（形状因子为极限1）作为选择的形状，仍然面临非常长的响应时间。也就是说矩形系数越好，分辨能力越细的滤波器实现成本越高，所以说，把一个理论上本来就很干净的正弦波检测为一根同样干净的细细的谱线，实现成本是非常巨大的，我们的工作就是在理想和现实之间寻找一个成本合适的平衡点：这个滤波器既要有良好的形状选择性，又要易于实现，还要对于各种测量场景（功率，噪声，分析等）表现较为一致的结果。
这时候高斯（Gaussian）滤波器闪亮登场了！是的，就是那个历史上最伟大没有之一的数学天才高斯，拿破仑东征曾经因为他在哥根廷大学执教而放弃了炮轰这座城市。我们小学时有高斯计算 1+2+3+...+99+100 等差数列的故事，中学时有高斯函数[x]，大学时有高斯分布，高斯不等式，高斯过程……那么频谱分析仪中的高斯滤波器是什么样子，为什么频谱分析仪的频率选择使用了高斯滤波器？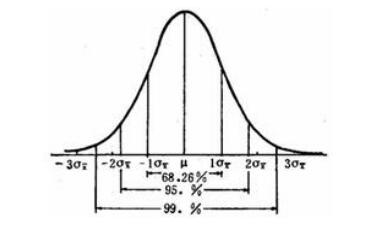
图 6 高斯分布曲线
形状选择有很多滤波器可供选择，例如通信中常见的升余弦滚降滤波器，常见分析仪器中有Hanning、Blackman、平顶滤波器、高斯滤波器等。通信系统中滤波器的目标是实现最小带宽下的无码间干扰，也就是根据奈奎斯特抽样准则设计的，用于通信调制信道的滤波器，这样的滤波器因为只考虑抽样判决时刻点，所以带宽较宽，截止较慢，过冲较大，脉冲形状难以控制。分析仪器中根据测量目的不同来选择滤波器，如果重点考虑幅度精度，最好使用平顶滤波器；如果重点考虑分辨率，最好使用Blackman滤波器等。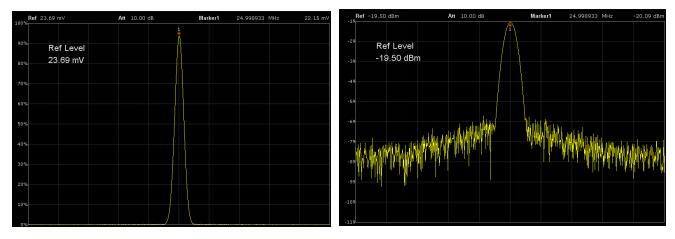
图 7 高斯滤波器的线性和对数形状
高斯滤波器有哪些优点适合频谱测量呢？总体来说，高斯滤波器可能不是选择性最好的，也不是实现最方便的，但是它在频域性能（理解为选择性或形状因子）和时域性能（理解为复杂度或响应速度）之间较为均衡。高斯滤波器的等效噪声带宽与其归一化的等效高斯带宽几乎相同，这是对噪声测量的一项重要需求指标；高斯滤波器的幅频响应是单瓣的，没有过零点的震荡，在各个方向上的平滑形状是完全相同的，这对于扫频测量幅度而不是相位是重要需求。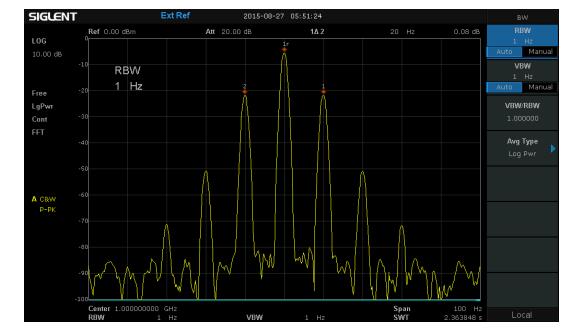
图 8在RBW=1Hz下的高斯形状滤波器
为什么不直接使用最小的高斯滤波器分辨率检测信号呢？这个问题的答案也呼之欲出。即使是使用高斯滤波器，仍然是越细致的分辨率响应时间越长。具体的时间公式如下：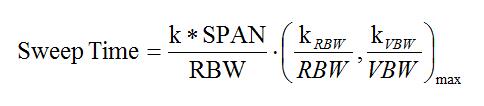
此式中，第一个因子的含义是在SPAN下进行频率选择的个数，每次的步进是RBW的1/k，以保证幅度测量的精度；第二个因子的含义是每次选择需要的时间，取决于RBW和VBW之间的较小值。通常当我们不关注噪声时，VBW常设置大于等于RBW，则时间公式简化为
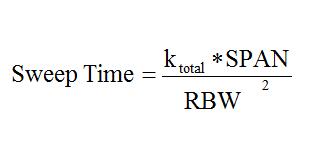也就是说扫描时间和SPAN成正比而和RBW的平方成反比，这意味着在相同SPAN的情况下RBW缩小100倍，扫描时间将扩大10000倍，因此在选择RBW的时候遵循够用的原则即可。
那么问题又来了，怎样才叫“够用”呢？RBW作为频谱分析仪最重要的指标之一，它的设置不仅影响着频率轴上的观察细节，也同样影响着幅度轴上的灵敏度，也就是底噪的高低。因此“够用”的选择标准要兼顾频率选择性，幅度选择性和扫描时间。
关于RBW和幅度底噪之间的关系我们将在后文详细阐述。在这里需要了解两个RBW设置之下底噪的高低变化规律是：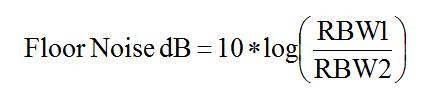
简单地说，RBW每变化10倍，底噪功率将变化10dB；RBW每变化3倍，底噪功率将变化约5dB，如图9所示，基于鼎阳科技SSA3032X频谱仪，我们设置不同的RBW，可以测量出底噪的差别很明显。较低的RBW有助于不同频率信号的分辨，同时使底噪降低，可以测量更低功率的信号，观察到更小的杂散，但是扫描时间将显著延长。较高的RBW有助于快速测量宽频带信号，但是将增加底噪，降低量测灵敏度，因此设置“够用”的RBW宽度是正确使用频谱分析仪重要的测试技巧。
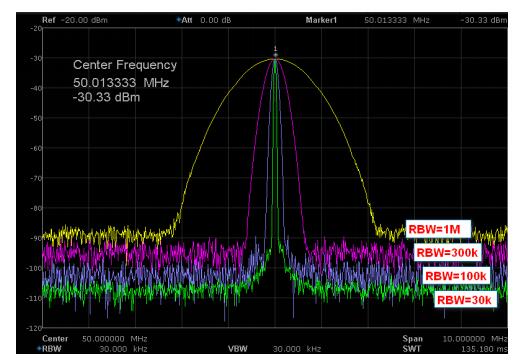
图 9不同RBW的底噪高低
在测量靠近中心频率的发射分量时，需要采用较窄的分辨带宽。RBW设置的大小能决定是否能把两个相临很近的信号分开，只有设置RBW大于或等于工作带宽时，读数才准确；但是如果信号太弱而底噪又太高，频谱仪则无法准确分辨信号，此时即使RBW大于工作带宽读数也会不准。
测试信道的功率或是链路噪声时，既不能太大，也不能太小，应该与信号的带宽相对应，一般的测试规范中会给出相应的RBW条件。分辨率带宽常小于参考信道的带宽时，测量结果应为参考带宽内各分量的总和（其和应为功率求?和，除非特别要求杂散信号按照电压求和），此时通常会使用频谱分析仪中Meas的Channel Power或ACPR等功能。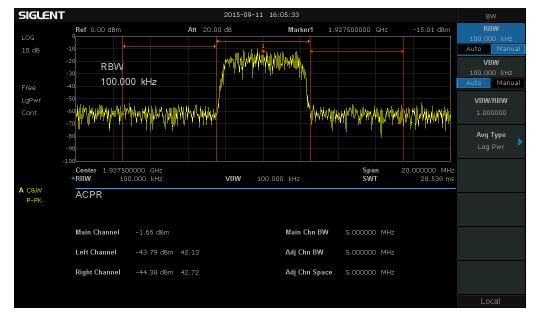
图 10 ACPR邻道功率比测量宽带信号的功率
还记得时间公式中被我们暂时忽略的视频带宽VBW（Video Bandwidth）么？VBW在频谱分析仪中的作用如何理解？
视频滤波是一个时域低通滤波，数学上等效于平均，效果上相当于平滑，是为了在反复的跳变噪声中平滑出趋势稳定的信号。视频滤波的带宽反映了平滑的程度，本来是这个时域滤波器的频域指标，之所以用频域指标，是为了和RBW配合使用，以方便在不同情况下的对比设置。
严格的说，VBW并不改变测量的结果，也不会参与“频率选择，峰值检测”的测量过程，它仅仅是数据在屏幕显示之前的一个移动平滑，对于结果的视觉效果有一定的影响。从下图中可以看到，当VBW很大时，起伏的噪声严重影响了小信号的显示，通过减小VBW，使小信号清晰地被辨了出来，而实际的频率分辨率和信号都没有发生改变，仅有随机噪声被平滑了下去，它提高了较低信噪比信号测量的分辨率和复现率，易于发现隐藏在噪声中的小信号。如图11所示，我们设置不同的VBW，可以看出通过平滑随机噪声，固定的小信号明显的从噪声中分离了出来。由于这里的平滑是通过平均的方式实现的，所以扫描时间也同步发生了变化，VBW越小就越平滑，因而平均次数越多，导致扫描时间成比例地扩大了。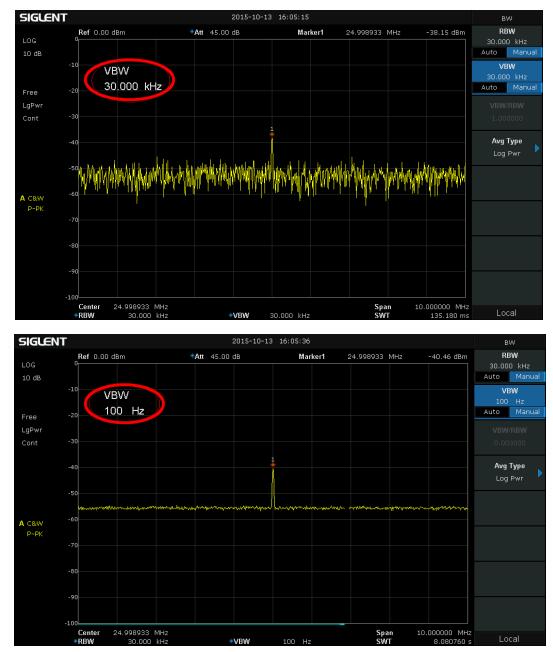
图 11 不同VBW对随机信号的平滑效果
通常的测量场景下，我们常常定义视分比（VBW/RBW）这个参数，通过两个带宽的联动来匹配相应的场景进行测量。
当噪声是测量的一部分时，诸如积分噪声（信道）功率，调制解调等场景，我们需要计算噪声的能量，此时要尽可能地使噪声全部参加运算，这时的VBW应大于RBW，以使噪声全部显示出来，即视分比大于1。或者完全不关心噪声时，也可以将视分比设置很大，以减小扫描时间。
当我们特别关注载波功率时，诸如测量杂散，边带噪声抑制比例等场景，就要尽量滤除噪声及其波动的影响，这时的VBW应远小于RBW，视分比远小于1，噪声平滑使测量结果稳定，但是会噪声扫描时间的增长。一般情况下视分比和RBW是自动关联的，为了兼顾扫描时间，通常默认为1。
以上对RBW和VBW这两种带宽的描述，仅着眼于频率分辨率和部分幅度分辨率的概念，完整的带宽和频率之间的关系分析，请看文章的后续篇《频谱分析仪应用解惑之频率分辨力》
关键词：频谱分析仪，频谱仪
分辨率带宽RBW(Resolution Bandwidth)，代表频谱分析仪将两个不同频率的信号清晰分辨出来的能力。两个不同频率的信号的距离如低于频谱分析仪的RBW，此时该两信号将部分重叠难以分辨。就像一幅图画在电脑上使用不同的分辨率去观察，清晰度是完全不同的。这里的“清晰”只是主观感受，普遍量化的标准是分辨率带宽定义在距离载波峰值衰减3dB的地方。在电磁干扰（EMI）测试标准中，分辨率带宽的标准为6dB。可以说6dB的选择性比3dB要强。
如图1所示是基于鼎阳科技SSA3032X频谱仪测量两个距离约20 kHz的单音信号，在使用带宽为30kHz，10kHz，3kHz的RBW观察时，这两个频率相近的信号测量的功率完全不变，信号被清晰分辨出来的程度是完全不同的。
图1 不同RBW的分辨能力
但是3dB带宽这个量化标准仍然是不够严谨，因为它只约束了3dB这一个点的位置。在相同的RBW下，还需要“矩形系数”这个参数，如图2所示。有的地方称为形状因子，就是衰减60dB时的带宽和衰减3dB时的带宽的比值。这个值越小越好，表明这个选择形状细长，能够将频率临近的信号完整地分离出来。一般来说，常见的数字频谱分析仪的矩形系数普遍为5：1左右。一个极端情况，如果3dB带宽和60dB带宽相同，那么矩形系数为1，这就是一个长方形了！
图 2 矩形系数示意
RBW的带宽和矩形系数，基本上决定了一个频谱分析仪的频率分辨能力，也就是将不等幅信号分辨出来的能力；反过来看，一旦RBW确定，那么是不能够观察到窄于RBW的频率谱线的。如图3所示，随着频率分辨能力的变化，两个临近的不等幅信号的分辨程度是不同的。
图3 RBW分辨不等幅信号的能力
当然，影响频谱分析仪频率分辨能力的因素不止这两个，在测量距离一个载波信号非常近的小信号时，即使RBW设置的相当小，也有可能分辨不出来。这是因为频率分辨能力还受到近端的相位噪声和本振的剩余调制的限制，这两点将在后续文章中阐述。
那么问题来了，为什么频谱分析仪的分辨率带宽的形状是一个脉冲的形状，而不能将理论上一个本来就很干净的正弦波检测为一根同样干净的细细的谱线？另一个相似的问题是，既然分辨率越清晰越好，为什么不直接使用最精细的分辨率带宽去检测信号？
面对这样的情况，一个训练有素的工程师对于很多理想化的测量场景，一定会给出的回答是：工程折中的实现。想以合适的代价得到测量结果，就不可避免丧失精度；反过来，想测得无比精确，结果就要付出很大成本才能得到。套用这个思路，我们给出一个官僚的解释：成本。
先回答第一个形状问题。这首先涉及到频谱分析仪的频率检测原理。从基础的角度考虑，我们可以把频谱分析仪理解为一种频率选择、峰值检测的电压表。“峰值检测”的表述，说明频谱分析仪的测量结果将是稳定的峰值，而不是变化的波形；“频率选择性”的表述，则说明频谱分析仪的对正弦波的频率是选择出来的，那么选择的方法其实就决定了频率分辨能力的大小。对于一些以FFT分析步进实现的频谱分析仪，只是每次选择的范围变大了一些，但是基本过程是没有根本变化的。
图 4 频域和时域的关系
在某个特定测量频率上看，我们对于频率的测量，就是用一个特定形状的滤波器去选频，一个细细的干净的正弦波经过选择滤波器，从而得到这个频率点的响应幅度，那么这个选择成型滤波器的选择能力就基本代表了频谱分析仪的频率选择能力。在整个频带测量过程上看，频谱分析仪的测量过程其实是使用穷举法，一个频点接一个频点地通过选择成型滤波器并测量峰值，然后遍历所有频点，拼凑出整个频率范围的能量分布。
图 5成型滤波器移动选择频率
如此来说，极端细致分辨能力的滤波器，相当于使用一个冲击函数去选择出需要的频率。如何构造一个冲击函数形状的滤波器呢，它在时域上是时间无穷幅度不变的，也就是不可能构造出来。退一步讲，使用一个矩形（形状因子为极限1）作为选择的形状，仍然面临非常长的响应时间。也就是说矩形系数越好，分辨能力越细的滤波器实现成本越高，所以说，把一个理论上本来就很干净的正弦波检测为一根同样干净的细细的谱线，实现成本是非常巨大的，我们的工作就是在理想和现实之间寻找一个成本合适的平衡点：这个滤波器既要有良好的形状选择性，又要易于实现，还要对于各种测量场景（功率，噪声，分析等）表现较为一致的结果。
这时候高斯（Gaussian）滤波器闪亮登场了！是的，就是那个历史上最伟大没有之一的数学天才高斯，拿破仑东征曾经因为他在哥根廷大学执教而放弃了炮轰这座城市。我们小学时有高斯计算 1+2+3+...+99+100 等差数列的故事，中学时有高斯函数[x]，大学时有高斯分布，高斯不等式，高斯过程……那么频谱分析仪中的高斯滤波器是什么样子，为什么频谱分析仪的频率选择使用了高斯滤波器？
图 6 高斯分布曲线
形状选择有很多滤波器可供选择，例如通信中常见的升余弦滚降滤波器，常见分析仪器中有Hanning、Blackman、平顶滤波器、高斯滤波器等。通信系统中滤波器的目标是实现最小带宽下的无码间干扰，也就是根据奈奎斯特抽样准则设计的，用于通信调制信道的滤波器，这样的滤波器因为只考虑抽样判决时刻点，所以带宽较宽，截止较慢，过冲较大，脉冲形状难以控制。分析仪器中根据测量目的不同来选择滤波器，如果重点考虑幅度精度，最好使用平顶滤波器；如果重点考虑分辨率，最好使用Blackman滤波器等。
图 7 高斯滤波器的线性和对数形状
高斯滤波器有哪些优点适合频谱测量呢？总体来说，高斯滤波器可能不是选择性最好的，也不是实现最方便的，但是它在频域性能（理解为选择性或形状因子）和时域性能（理解为复杂度或响应速度）之间较为均衡。高斯滤波器的等效噪声带宽与其归一化的等效高斯带宽几乎相同，这是对噪声测量的一项重要需求指标；高斯滤波器的幅频响应是单瓣的，没有过零点的震荡，在各个方向上的平滑形状是完全相同的，这对于扫频测量幅度而不是相位是重要需求。
图 8在RBW=1Hz下的高斯形状滤波器
为什么不直接使用最小的高斯滤波器分辨率检测信号呢？这个问题的答案也呼之欲出。即使是使用高斯滤波器，仍然是越细致的分辨率响应时间越长。具体的时间公式如下：
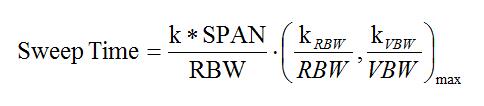
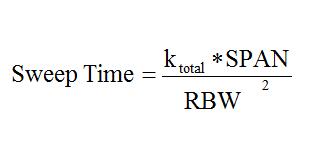
那么问题又来了，怎样才叫“够用”呢？RBW作为频谱分析仪最重要的指标之一，它的设置不仅影响着频率轴上的观察细节，也同样影响着幅度轴上的灵敏度，也就是底噪的高低。因此“够用”的选择标准要兼顾频率选择性，幅度选择性和扫描时间。
关于RBW和幅度底噪之间的关系我们将在后文详细阐述。在这里需要了解两个RBW设置之下底噪的高低变化规律是：
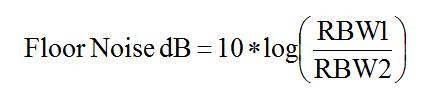
图 9不同RBW的底噪高低
在测量靠近中心频率的发射分量时，需要采用较窄的分辨带宽。RBW设置的大小能决定是否能把两个相临很近的信号分开，只有设置RBW大于或等于工作带宽时，读数才准确；但是如果信号太弱而底噪又太高，频谱仪则无法准确分辨信号，此时即使RBW大于工作带宽读数也会不准。
测试信道的功率或是链路噪声时，既不能太大，也不能太小，应该与信号的带宽相对应，一般的测试规范中会给出相应的RBW条件。分辨率带宽常小于参考信道的带宽时，测量结果应为参考带宽内各分量的总和（其和应为功率求?和，除非特别要求杂散信号按照电压求和），此时通常会使用频谱分析仪中Meas的Channel Power或ACPR等功能。
图 10 ACPR邻道功率比测量宽带信号的功率
还记得时间公式中被我们暂时忽略的视频带宽VBW（Video Bandwidth）么？VBW在频谱分析仪中的作用如何理解？
视频滤波是一个时域低通滤波，数学上等效于平均，效果上相当于平滑，是为了在反复的跳变噪声中平滑出趋势稳定的信号。视频滤波的带宽反映了平滑的程度，本来是这个时域滤波器的频域指标，之所以用频域指标，是为了和RBW配合使用，以方便在不同情况下的对比设置。
严格的说，VBW并不改变测量的结果，也不会参与“频率选择，峰值检测”的测量过程，它仅仅是数据在屏幕显示之前的一个移动平滑，对于结果的视觉效果有一定的影响。从下图中可以看到，当VBW很大时，起伏的噪声严重影响了小信号的显示，通过减小VBW，使小信号清晰地被辨了出来，而实际的频率分辨率和信号都没有发生改变，仅有随机噪声被平滑了下去，它提高了较低信噪比信号测量的分辨率和复现率，易于发现隐藏在噪声中的小信号。如图11所示，我们设置不同的VBW，可以看出通过平滑随机噪声，固定的小信号明显的从噪声中分离了出来。由于这里的平滑是通过平均的方式实现的，所以扫描时间也同步发生了变化，VBW越小就越平滑，因而平均次数越多，导致扫描时间成比例地扩大了。
图 11 不同VBW对随机信号的平滑效果
通常的测量场景下，我们常常定义视分比（VBW/RBW）这个参数，通过两个带宽的联动来匹配相应的场景进行测量。
当噪声是测量的一部分时，诸如积分噪声（信道）功率，调制解调等场景，我们需要计算噪声的能量，此时要尽可能地使噪声全部参加运算，这时的VBW应大于RBW，以使噪声全部显示出来，即视分比大于1。或者完全不关心噪声时，也可以将视分比设置很大，以减小扫描时间。
当我们特别关注载波功率时，诸如测量杂散，边带噪声抑制比例等场景，就要尽量滤除噪声及其波动的影响，这时的VBW应远小于RBW，视分比远小于1，噪声平滑使测量结果稳定，但是会噪声扫描时间的增长。一般情况下视分比和RBW是自动关联的，为了兼顾扫描时间，通常默认为1。
以上对RBW和VBW这两种带宽的描述，仅着眼于频率分辨率和部分幅度分辨率的概念，完整的带宽和频率之间的关系分析，请看文章的后续篇《频谱分析仪应用解惑之频率分辨力》
关键词：频谱分析仪，频谱仪
上一篇 : 浅析示波器的存储深度
下一篇 : 示波器的带宽越高越好吗?
